MathMLマニュアル

4. MathML Tips集

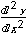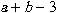
4.1 足し算や引き算

足し算や引き算を書く場合は, 3. MathMLの書き方で示したように以下のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>+</mo>
  <mi>b</mi>
  <mo>-</mo>
  <mn>3</mn>
</math>

リスト4.1 足し算や引き算

図4.1 足し算や引き算の表示例

4.2 かけ算

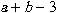
一般に数学では, 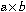のようなかけ算を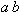と表します. これをMathMLで表示するには, InvisibleTimesと言う実体参照とmoを利用して, 次のように書く必要があります.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>&InvisibleTimes;</mo>
  <mi>b</mi>
</math>

リスト4.2 かけ算

図4.2 かけ算の表示例

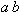
<mi>ab</mi>や<mi>a</mi><mi>b</mi>と書いても, 図4.2と同様に表されるかもしれません. しかし, これらの書き方は, かけ算を意味しておらず, 場合によっては, 表示のされ方が異なります(上の例では, aとbの間の広さが異なる可能性があります). ですから, <mo>⁢</mo>という実体参照を使うべきです.

4.3 分数

分数を書くには, mfracを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfrac>
    <mn>1</mn>
    <mn>2</mn>
  </mfrac>
  <mo>+</mo>
  <mfrac>
    <mn>1</mn>
    <mi>x</mi>
  </mfrac>
  <mo>-</mo>
  <mfrac>
    <mi>x</mi>
    <mn>3</mn>
  </mfrac>
</math>

リスト4.3 分数

図4.3 分数の表示例

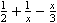
mfracの中には, 2つのタグを入れます. 1つめのタグが分子を表し, 2つめのタグが分母を表します. 分子や分母には, 上の例のようにmoやmiといったタグを入れることができます. この他にも, mrowやmsub,msup,mover,munder・・・など多様なタグを入れることができます.

4.4 式をかっこで囲む

式をかっこで囲む場合, moを利用して, 次のように書くことができます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>+</mo>
  <mo>(</mo>
  <mi>b</mi>
  <mo>-</mo>
  <mn>3</mn>
  <mo>)</mo>
</math>

リスト4.4 式をかっこで囲む(mo)

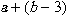
図4.4 式をかっこで囲む(mo)の表示例

また, 式をかっこで囲む場合, mfencedとmrowを利用して, 次のように書くこともできます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>+</mo>
  <mfenced>
    <mrow>
      <mi>b</mi>
      <mo>-</mo>
      <mn>3</mn>
    </mrow>
  </mfenced>
</math>

リスト4.5 式をかっこで囲む(mfenced)

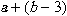
図4.5 式をかっこで囲む(mfenced)

mfencedの中のmrowは書く必要があります. 書かないと, mfencedの中身が, カンマ区切りで表示されます. 詳しくは, 4.23 ベクトルの成分を見てください

4.5 分数の分子や分母に式を入れる

分数の分子や分母に式を入れるに場合, mrowを分子, または分母として記述し, その中に式を書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfrac>
    <mrow>
      <mi>x</mi>
      <mo>-</mo>
      <mn>1</mn>
    </mrow>
    <mn>3</mn>
  </mfrac>
  <mo>+</mo>
  <mfrac>
    <mi>1</mi>
    <mrow>
      <mi>a</mi>
      <mo>+</mo>
      <mi>b</mi>
    </mrow>
  </mfrac>
  <mo>-</mo>
  <mfrac>
    <mrow>
      <mi>x</mi>
      <mo>+</mo>
      <mn>3</mn>
    </mrow>
    <mrow>
      <mi>x</mi>
      <mo>-</mo>
      <mi>c</mi>
    </mrow>
  </mfrac>
</math>

リスト4.6 分数の分子や分母に式を入れる

図4.6 分数の分子や分母に式を入れる場合の表示例

4.6 累乗

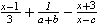
累乗を書く場合, msupを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mi>x</mi>
    <mn>2</mn>
  </msup>
  <mo>-</mo>
  <msup>
    <mn>3</mn>
    <mi>x</mi>
  </msup>
</math>

リスト4.7 累乗

図4.7 累乗の表示例

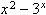
msupの中には, 2つのタグを入れます. 1つめのタグが底を表し, 2つめのタグが指数を表します. 底や指数には, 上の例のようにmoやmiといったタグを入れることができます. この他にも, mrowやmfencedやmsub・・・などを入れることができます.

4.7 式の累乗

式の累乗を書く場合, msupの中の1つめのタグとしてmfencedを書き, その中にmrowを書き, その中に式を書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mfenced>
      <mrow>
        <mi>x</mi>
        <mo>+</mo>
        <mn>3</mn>
      </mrow>
    </mfenced>
    <mn>3</mn>
  </msup>
</math>

リスト4.8 式の累乗

図4.8 式の累乗の表示例

4.8 平方根

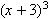
平方根を書くには, msqrtを利用して次のように書きます

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msqrt>
    <mi>x</mi>
  </msqrt>
  <mo>+</mo>
  <msqrt>
    <mn>2</mn>
  </msqrt>
</math>

リスト4.9 平方根

図4.9 平方根の表示例

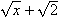
msqrtの中には, 上の例のようにmiやmnといったタグを入れることができます. この他にも, mrowやmsubのようなタグを入れることができます.

4.9 式の平方根

式の平方根を書くには, msqrtを書き, その中にmrowを書き, その中に式を書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msqrt>
    <mrow>
      <msup>
        <mi>x</mi>
        <mn>2</mn>
      </msup>
      <mo>+</mo>
      <mn>3</mn>
    </mrow>
  </msqrt>
</math>

リスト4.10 式の平方根

図4.10 式の平方根

4.10 等号や不等号

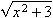
等号や不等号を書くには, 全てmoを使います. ">"にはgt, "<"にはlt, "≥"にはge, "≤"にはleという実体参照をそれぞれ使います.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>=</mo>
  <mi>b</mi>
</math>
<br/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>&gt;</mo>
  <mi>b</mi>
</math>
<br/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>&ge;</mo>
  <mi>b</mi>
</math>
<br/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>&lt;</mo>
  <mi>b</mi>
</math>
<br/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>a</mi>
  <mo>&le;</mo>
  <mi>b</mi>
</math>

リスト4.11 等号や不等号

図4.11 等号や不等号の表示例

4.11 添字

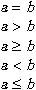
添字を書くには, msubを利用して次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msub>
    <mi>x</mi>
    <mn>3</mn>
  </msub>
  <mo>&InvisibleTimes;</mo>
  <msub>
    <mi>r</mi>
    <mi>x</mi>
  </msub>
</math>

リスト4.12 添字

図4.12 添字の表示例

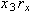
msubの中には, 2つのタグを入れます. 2つめのタグが, 1つめのタグに付く添字になります. 添字には, 上の例のようにmoやmiといったタグを入れることができます. この他にも, mrowなどを入れることができます.

4.12 関数`f(x)`

関数f(x)を表現するには, ApplyFunctionという実体参照とmoを利用して, 次のように書く必要があります.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>f</mi>
  <mo>&ApplyFunction;</mo>
  <mfenced>
    <mrow>
      <mi>x</mi>
    </mrow>
  </mfenced>
</math>

リスト4.13 関数f(x)

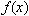
図4.13 関数f(x)の表示例

関数名であるfはmiで囲みます. <mo>⁡</mo>は, moの前に書かれた関数をmoの後に書かれた数に適用するということを意味しています. また, mfencedという表現は, moを用いて次のように表すこともできます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>f</mi>
  <mo>&ApplyFunction;</mo>
  <mrow>
    <mo>(</mo>
    <mi>x</mi>
    <mo>)</mo>
  </mrow>
</math>

リスト4.14 moを用いた関数f(x)

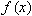
図4.14 moを用いた関数f(x)の表示例

4.13 指数に式を入れる

指数に式を入れるには, msupの中の2つめのタグとしてmrowを書き, その中に式を書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mi>x</mi>
    <mrow>
      <mi>y</mi>
      <mo>-</mo>
      <mfrac>
        <mn>1</mn>
        <mn>3</mn>
      </mfrac>
    </mrow>
  </msup>
</math>

リスト4.15 指数に式を入れる

図4.15 指数に式を入れる場合の表示例

4.14 累乗根

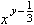
累乗根を書くには, mrootを利用して次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mroot>
    <mi>x</mi>
    <mn>3</mn>
  </mroot>
  <mo>+</mo>
  <mroot>
    <mn>3</mn>
    <mi>a</mi>
  </mroot>
</math>

リスト4.16 累乗根

図4.16 累乗根の表示例

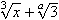
mrootの中には, 2つのタグを入れます. 1つめのタグが底を表し, 2つめのタグが指数を表します. 底や指数には, 上の例のように, moやmiといったタグを入れることができます. この他にもmrowなどを入れることができます.

4.15 三角関数

三角関数を書くには, ApplyFunctionというう実体参照を使って次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>sin</mi>
  <mo>&ApplyFunction;</mo>
  <mfenced>
    <mrow>
      <mi>x</mi>
      <mo>+</mo>
      <mn>3</mn>
    </mrow>
  </mfenced>
</math>

リスト4.17 三角関数

図4.17 三角関数の表示例

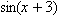
他の三角関数を使用するには, sinのところを, cos, tan, sec, cosec, cotに変更します.

4.16 円周率π

円周率πを表示するには, piという実体参照とmiを利用して次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>&pi;</mi>
</math>

リスト4.18 円周率π

図4.18 円周率πの表示例

4.17 対数関数

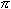
対数関数を書くには, 関数名のところにmsubを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/MathMathML">
  <msub>
    <mi>log</mi>
    <mn>3</mn>
  </msub>
  <mo>&ApplyFunction;</mo>
  <mi>x</mi>
</math>

リスト4.19 対数関数

図4.19 対数関数の表示例

4.18 ネピアーの数e

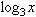
ネピアーの数eを書くには, ExponentialEという実体参照とmiを利用します. 例えば, 自然対数関数やネピアーの数を底とする指数関数は, 次のように書かれます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msub>
    <mi>log</mi>
    <mi>&ExponentialE;</mi>
  </msub>
  <mo>&ApplyFunction;</mo>
  <mi>x</mi>
  <mo>+</mo>
  <msup>
    <mi>&ExponentialE;</mi>
    <mi>x</mi>
  </msup>
</math>

リスト4.20 ネピアーの数e

図4.20 ネピアーの数eの表示例

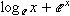
<mi>e</mi>と書いても, eと表示されますが, ネピアーの数であることを明示的に表すために, ExponentialEという実体参照を使うべきです.

4.19 逆三角関数

逆三角関数を書くには, 関数名のところにmsupを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msup>
    <mi>sin</mi>
    <mn>-1</mn>
  </msup>
  <mo>&ApplyFunction;</mo>
  <mi>x</mi>
</math>

リスト4.21 逆三角関数

図4.21 逆三角関数の表示例

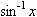
他の逆三角関数を使用するには, sinのところを, cos, tan, sec, cosec, cotに変更します.

4.20 和の記号∑

和の記号∑を表すには, sumという実体参照と, munderoverを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <munderover>
    <mi>&sum;</mi>
    <mrow>
      <mi>i</mi>
      <mo>=</mo>
      <mn>1</mn>
    </mrow>
    <mn>20</mn>
  </munderover>
  <msub>
    <mi>k</mi>
    <mi>i</mi>
  </msub>
</math>

リスト4.22 和の記号∑

図4.22 和の記号∑の表示例

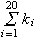
munderoverには, 3つのタグを入れます. 1つめのタグがまん中, 2つめのタグが下側, 3つめのタグが上側に表示されます. munderoverの中には, 上の例のように, mi,mn,mrowなどのタグを入れることができます.

4.21 順列, 組合せ

順列や組合せを書くには, mmultiscriptsを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mmultiscripts>
    <mi>P</mi>
    <mi>r</mi>
    <none/>
    <mprescripts/>
    <mi>n</mi>
    <none/>
  </mmultiscripts>
</math>
<br/>
<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mmultiscripts>
    <mi>C</mi>
    <mn>5</mn>
    <none/>
    <mprescripts/>
    <mn>2</mn>
    <none/>
  </mmultiscripts>
</math>

リスト4.23 順列, 組合せ

図4.23 順列, 組合せの表示例

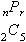
mmultiscriptsは, 左や右に上付や下付の文字を付けるためのタグです. 構文は, 複雑なので, ここでは説明しません. 詳しくは, MathMLの仕様書を見てください. 順列や組合せを書く場合に上のような構文を用いると考えてください.

4.22 ベクトル

ベクトルを書くには, RIghtArrorという実体参照とmo及びmoverを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mover>
    <mi>v</mi>
    <mo>&RightArrow;</mo>
  </mover>
</math>

リスト4.24 ベクトル

図4.24 ベクトル

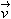
moverには, 2つのタグを入れます. 1つめのタグ上側に, 2つめのタグが表示されます.

4.23 ベクトルの成分

ベクトルの成分を書くには, mfencedを用いて次のように書くことができます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfenced>
    <msub>
      <mi>a</mi>
      <mi>x</mi>
    </msub>
    <mrow>
      <msub>
        <mi>a</mi>
        <mi>y</mi>
      </msub>
      <mo>+</mo>
      <msub>
        <mi>b</mi>
        <mi>y</mi>
      </msub>
    </mrow>
  </mfenced>
</math>

リスト4.25 mfencedを用いたベクトルの成分

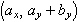
図4.25 mfencedを用いたベクトルの成分の表示例

mfencedは, 4.4 式をかっこで囲むで使ったように, かっこで囲むためのタグですが, 上の例のように, 中に複数のタグを入れることで, それらをカンマ区切りで表示することが可能です. mfencedの中には, 上の例のようにmsubやmrowを入れることができます. またmiやmn・・・など多様なタグを入れることができます.

また, ベクトルの成分を書くには, moを利用して, 次のように書くこともできます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mo>(</mo>
  <msub>
    <mi>a</mi>
    <mi>x</mi>
  </msub>
  <mo>,</mo>
  <mrow>
    <msub>
      <mi>a</mi>
      <mi>y</mi>
    </msub>
    <mo>+</mo>
    <msub>
      <mi>b</mi>
      <mi>y</mi>
    </msub>
  </mrow>
  <mo>)</mo>
</math>

リスト4.26 moを用いたベクトルの成分

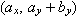
図4.26 moを用いたベクトルの成分の表示例

4.24 行列

行列を書くには, mfencedとmtableを用いて, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfenced>
    <mtable>
      <mtr>
        <mtd>
          <mi>x</mi>
        </mtd>
        <mtd>
          <mn>3</mn>
        </mtd>
      </mtr>
      <mtr>
        <mtd>
          <mrow>
            <mo>-</mo>
            <mn>1</mn>
          </mrow>
        </mtd>
        <mtd>
          <mi>y</mi>
        </mtd>
      </mtr>
    </mtable>
  </mfenced>
</math>

リスト4.27 行列

図4.27 行列の表示例

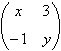
mtableは, HTMLのtableに似たタグで, 中に, HTMLのtrにあたるmtr, その中に, HTMLのtdにあたるmtdをいれ, 表のように表示します. mtdの中には, 上の例のように, miやmnやmrowを入れることができます. この他にも, msubやmsup・・・などのタグを入れることができます.

4.25 行列式

行列式を書くには, mfencedのopen属性やclose属性を利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfenced open="|" close="|">
    <mtable>
      <mtr>
        <mtd>
          <mn>2</mn>
        </mtd>
        <mtd>
          <mn>3</mn>
        </mtd>
      </mtr>
      <mtr>
        <mtd>
          <mn>4</mn>
        </mtd>
        <mtd>
          <mn>5</mn>
        </mtd>
      </mtr>
    </mtable>
  </mfenced>
</math>

リスト4.28 行列式

図4.28 行列式の表示例

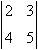
mfencedのopen属性は左側のかっこの形を表し, close属性は右側のかっこの形を表します.

4.26 微分

微分記号dを書くには, DifferentialDという実体参照とmoを利用します. 例えば, yのxによる微分は, 次のように書かれます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfrac>
    <mrow>
      <mo>&DifferentialD;</mo>
      <mi>y</mi>
    </mrow>
    <mrow>
      <mo>&DifferentialD;</mo>
      <mi>x</mi>
    </mrow>
  </mfrac>
</math>

リスト4.29 微分

図4.29 微分の表示例

4.27 不定積分

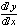
積分記号∫を書くには, intという実体参照とmoを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mo>&int;</mo>
  <mrow>
    <mfenced>
      <mrow>
        <mi>x</mi>
        <mo>+</mo>
        <mn>1</mn>
      </mrow>
    </mfenced>
    <mo>&InvisibleTimes;</mo>
    <mrow>
      <mo>&DifferentialD;</mo>
      <mi>x</mi>
    </mrow>
  </mrow>
</math>

リスト4.30

図4.30 不定積分の表示例

4.28 定積分

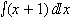
定積分を書くには, msubsupを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msubsup>
    <mo>&int;</mo>
    <mn>0</mn>
    <mi>&pi;</mi>
  </msubsup>
  <mrow>
    <mi>cos</mi>
    <mo>&ApplyFunction;</mo>
    <mi>x</mi>
    <mo>&InvisibleTimes;</mo>
    <mrow>
      <mo>&DifferentialD;</mo>
      <mi>x</mi>
    </mrow>
  </mrow>
</math>

リスト4.31 定積分

図4.31 定積分

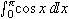
msubsupは, 3つのタグを入れます. 1つめのタグに対して, 2つめのタグが上付, 3つのタグが下付で表示されます. msubsupの中のタグには, 上の例のように, moやmiやmnを入れることができます. この他にも, mrowやmfenced・・・など多様なタグを入れることができます.

4.29 無限大

無限大を書くには, infinという実体参照とmiを利用します. 例えば, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <msubsup>
    <mo>&int;</mo>
    <mn>1</mn>
    <mi>&infin;</mi>
  </msubsup>
  <mfrac>
    <mrow>
      <mo>&DifferentialD;</mo>
      <mi>x</mi>
    </mrow>
    <msup>
      <mi>x</mi>
      <mn>2</mn>
    </msup>
  </mfrac>
</math>

リスト4.32 無限大

図4.32 無限大の表示例

4.30 絶対値

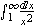
絶対値を書くには, mfencedのopen属性やclose属性を利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfenced open="|" close="|">
    <mrow>
      <mo>-</mo>
      <mi>a</mi>
    </mrow>
  </mfenced>
</math>

リスト4.33 mfencedを用いた絶対値

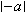
図4.33 mfencedを用いた絶対値の表示例

mfencedのopen属性やclose属性については, 4.25 行列式を見て下さい. また, mfencedを使わずに, moを用いて次のように表すこともできます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mo>|</mo>
  <mrow>
    <mo>-</mo>
    <mi>a</mi>
  </mrow>
  <mo>|</mo>
</math>

リスト4.34 moを用いた絶対値

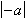
図4.34 moを用いた絶対値の表示例

4.31 複号

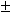といった複号を書く場合は, PlusMinusという実体参照とmoを利用して, また, 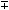といった複合を書く場合は, MinusPlusという実体参照とmoを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mi>x</mi>
  <mo>&PlusMinus;</mo>
  <mi>y</mi>
  <mo>&MinusPlus;</mo>
  <mn>3</mn>
</math>

リスト4.35 複号

図4.35 複号の表示例

4.32 極限

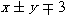
極限を書く場合には, munderを利用して次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <munder>
    <mi>lim</mi>
    <mrow>
      <mi>x</mi>
      <mo>&RightArrow;</mo>
      <mn>0</mn>
    </mrow>
  </munder>
  <mrow>
    <mi>sin</mi>
    <mo>&ApplyFunction;</mo>
    <mi>x</mi>
  </mrow>
</math>

リスト4.36

図4.36 極限の表示例

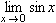
munderには, 2つのタグを入れます. 1つめのタグの下側に, 2つめのタグが表示されます.

4.33 虚数

虚数iを書くには, ImaginaryIという実体参照とmiを利用して, 次のように書きます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mn>4</mn>
  <mo>+</mo>
  <mn>3</mn>
  <mo>&InvisibleTimes;</mo>
  <mi>&ImaginaryI;</mi>
</math>

リスト4.37 虚数

図4.37 虚数の表示例

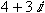
<mi>i<mi>と書いても, iと表示されますが, 虚数ということを明確に表すため, ImaginaryIという実体参照を使うべきです.

4.34 偏微分

偏微分記号∂を書くには, partという実体参照とmoを利用します. 例えば, zのxによる偏微分は, 次のように書かれます.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfrac>
    <mrow>
      <mo>&part;</mo>
      <mi>z</mi>
    </mrow>
    <mrow>
      <mo>&part;</mo>
      <mi>x</mi>
    </mrow>
  </mfrac>
</math>

リスト4.38 偏微分

図4.38 偏微分の表示例

4.35 2階微分

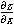
2階微分を書くには, DifferentialDという実体参照とmo,msupを利用します. 例えば, yのxによる2階微分は次のようになります.

<math xmlns="http://www.w3.org/1998/Math/MathML">
  <mfrac>
    <mrow>
      <msup>
        <mo>&DifferentialD;</mo>
        <mn>2</mn>
      </msup>
      <mi>y</mi>
    </mrow>
    <msup>
      <mrow>
        <mo>&DifferentialD;</mo>
        <mi>x</mi>
      </mrow>
      <mn>2</mn>
    </msup>
  </mfrac>
</math>

リスト4.39 2階微分

図4.39 2階微分の表示例